CALCULATE TOTAL DYNAMIC HEAD (TDH) AND NET POSITIVE SUCTION HEAD (NPSH)
The two most critical values that must be calculated for a pump system are Total Dynamic Head (TDH) and Net Positive Suction Head (NPSH). A simple guide to these calculations follows.
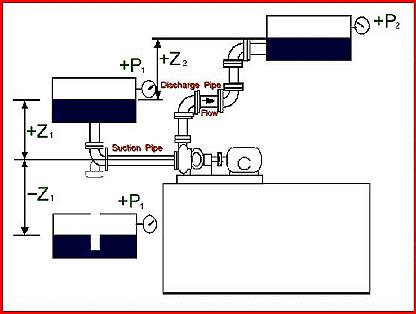
All symbols noted in the calculations are referenced in the sketch shown above
P2 = Pressure on liquid surface in discharge tank in psia (see P2 above) P1 = Pressure on liquid surface in suction tank in psia (see P1 above) Z2 = Height in feet of liquid surface in discharge tank, above surface in suction tank Hfs = Friction loss in feet in suction line, as above Hfd = Friction loss in feet in discharge line including exit loss from pipe into tank
The gallons per minute (GPM) required and total head (TDH), as determined above, can be used directly on the pump performance curves to make the proper pump selection. Remember that the total head developed by a pump and its NPSH required is the same for all specific gravities. After selecting a pump for the proper GPM and TDH, check that the available NPSH (NPSHA) is greater than the required NPSH (NPSHR) of the pump.
TOTAL DYNAMIC HEAD = (P2 – P1) x 2.31 Specific Gravity + Z2 + Hfs + Hfd
To determine the horsepower required, the following formula can be used:
BRAKE HORSEPOWER REQUIRED = (GPM x TDH x Specific Gravity) / (3960 x Pump Efficiency)
Click Here for Temperature-Vapor Pressure for Water Table
Net Positive Suction Head – Amount of energy in the liquid at the pump datum. It must be defined to have a meaning, as either available or required NPSH.
Required NPSH – A characteristic of the pump design. It is determined by test or computation and is the energy needed to fill a pump on the suction side and overcome the friction and low losses from the suction connection to that point in the pump at which more energy is added. Required NPSH varies with pump design, pump size and operating conditions and is supplied by the pump manufacturer.
Available NPSH– A characteristic of the system and is defined as the energy which is in a liquid at the suction connection of the pump (regardless of the type of pump) over and above that energy in the liquid due to its vapor pressure. Available NPSH can be calculated or obtained by taking test readings at the suction side of the pump.
Available NPSH = (P1 – Pv) 2.31 Specific Gravity + Z1 – Hfs
P1 = Pressure on liquid surface in pounds per square inch absolute (psia). Absolute pressure is equal to gauge reading plus atmospheric pressure. Three common examples are:
Open tank – No gauge reading so absolute pressure equals atmospheric pressure, or 14.7 psia at sea level. Closed tank under pressure – Add gauge reading in psig to atmospheric pressure to get total absolute pressure. Closed tank under vacuum- Subtract vacuum reading in inches of mercury from atmospheric pressure in inches of mercury (30 inches at sea level) and convert to psia by multiplying by .49.
Pv = Vapor pressure of liquid in psia at pumping temperature. Available from data tables.
Sp.Gr. = Specific gravity of liquid being handled.
Z1 = Height of liquid surface above pump suction, measure in feet. If surface is below pump, use minus sign.
Hfs = Friction loss in feet suction pipe including entrance loss from tank to pipe, and loss in all valves, elbows, and other fittings.
Cavitation: When the NPSH required by the pump is greater than the NPSH available by the system, cavitation occurs. Vapor is formed and moves along with the stream. These vapor bubbles or “cavities” collapse when they reach regions or higher pressure on their way through the pump.
The most obvious effects of cavitation are noise and vibration. This is caused by the collapse of the vapor bubbles as they reach the high pressure side of the pump. The bigger the pump, the greater the noise and vibration. If operating under cavitating conditions for a sufficient length of time, especially on water service, impeller vane pitting will take place. The violent collapse of vapor bubbles forces liquid at high velocity into vapor filled pores of the metal, producing surge pressures of high intensity on small areas. These pressures can exceed the tensile strength of the metal, and actually blast out particles, giving the metal a spongy appearance. This noise and vibration can cause bearing failure, shaft breakage and other fatigue failures in the pump.





